|
|
|
|
|
|
|
Figure 6.19
Splitting requests. |
|
|
|
|
|
|
|
|
6.5.1 The Open-Queue (Flores) Memory Model |
|
|
|
|
|
|
|
|
We can use open-queueing theory as an approximation to interleaved memory behavior by assuming a request rate independent of the service behavior. This allows us to find an initial partition of memory modules. This model was originally proposed by Flores [90] using the M/D/1 queue. We use the more appropriate MB/D/1 queue model. |
|
|
|
|
|
|
|
|
Let ls be the total request rate (processor and I/O) in requests/second. |
|
|
|
|
|
|
|
|
Assume that ls splits m ways uniformly over the m modules. Then, at the module: |
|
|
|
|
|
|
|
|
and 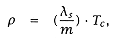 |
|
|
|
|
|
|
|
|
and we now can use the MB/D/1 model to determine Tw and Qo (the per module buffer size). |
|
|
|
|
|
|
|
|
Design with the Flores Model |
|
|
|
|
|
|
|
|
1. Find peak processor (design) instruction execution rate measured in MIPS (million instructions per second). Again, we use peak rates so that the memory system is designed to support such execution rates. The memory system lowers processor performance in any event, when offered the peak rate due to contention. |
|
|
|
|
|
|
|
|
2. MIPS * (references/instruction) + MIPS *(I/O references/instruction) = MAPS (million accesses per second). |
|
|
|
|
|
|
|
|
3. As a balance between cost or interleaving factor and performance, choose m so that r» 0.5 and also so that m = 2k (k an integer). |
|
|
|
|
|
|
|
|
4. Tw + Ta = total memory access time. |
|
|
|
|
|
|
|
|
5. Note that this model predicts the total average open-queue size as Qo-t = mQo. |
|
|
|
|
|