|
|
|
|
|
|
|
This is commonly referred to as the Pollaczek-Khinchine (or P-K) meanvalue result. (See Appendix ?? for a derivation of this equation.) We can select c2 for several cases of interest. In the first case, the service time is exponentially distributed 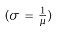 and c2 = 1. This might correspond to a model of an I/O server. and c2 = 1. This might correspond to a model of an I/O server. |
|
|
|
|
|
|
|
|
In the second case, as in memory, the service time is constant and c2 = 0. For this case, we have: |
|
|
|
|
|
|
|
|
For MB/D/1: (Binomial arrival, constant service) |
|
|
|
 |
|
|
|
|
c2 = 0. |
|
|
|
|
|
|
|
|
If r < p, then Tw»0; Qo» 0. (In simple memory-processor models, the case r < p should not arise, since at least one processor request is assumed each memory cycle; a more general model, discussed later, is usually more appropriate to statistically distributed processor requests that accommodate r < p.) |
|
|
|
|
|
|
|
|
For M/G/1, multiple (independent, Poisson) sources generate requests. A different service time can be assigned to the requests of each source. (Note there is still a single server.) This model allows us to split the request stream into smaller streams, capturing more detail. The M/G/1 model has a simple solution wherein effective request and service rates are calculated. The M/G/1 formulation for two sources, (l1, T1) and (l2,T2), is given next (multiple sources are calculated in a similar manner): |
|
|
|
|
|
|
|
|
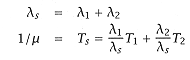 (6.1) (6.1) |
|
|
|
|
|