|
|
|
| Table 1.3 Comparison of floating-point specifications. |
| | | | | | | | | | | | | | Word length | | | | | | | | | Exponent | | | | | | | | | Significand | | | | | | | | | Bias of exponent | | | | | Radix | | | | | Hidden "1" | | | | | Radix point | | | | | Range of Fraction | | | | | F representation | | | | | Approximate max. positive number | 1663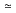 1076 1076 |
| 2126* 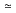 1038 1038 |
| 21024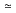 10308 (L) 10308 (L) |
| | Precision | S: 16-6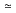 10-7 10-7 |
| S: 2-24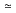 10-7 10-7 |
| S : 2-23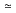 10-7 10-7 |
| | L: 16-14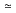 10-17 10-17 |
| L: 2-56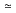 10-17 10-17 |
| L: 2-52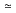 10-16 10-16 |
| | *Approximate maximum positive number, excluding reserved exponent representations. | | **MSBmost significant bit. |
|
|
|
|
|
|
2. Reals (both fixed- and floating-point representations). |
|
|
|
 |
|
|
|
|
Fixed point consists of both integer and fractional portions of fixed sizes that are manipulated much as integers (they are often called scaled integers), and yet represent non-integral values. The advantage of fixed-point numbers is that they provide real values with no overhead other than conversion over their limited range (determined by the fixed field sizes). One benefit of this representation is that the numbers may be treated in the software as if they were integers. Floating-point numbers are represented by a fractional value with an exponent multiplier. These numbers require significant conversion as well as care during some operations to ensure that numbers are "compatible" both before and after the operation (called normalization). The main advantage of floating-point numbers is the large range of numbers availablethe IEEE double precision format can represent numbers from 2.2 ´ 10-308 up to 1.8 ´ 10308. For comparison, a 64b fixed-point number would have a maximum representation of about 1020. |
|
|
|
 |
|
|
|
|
Floating-point numbers have a number of different representations; the most common systems include those used in System 390, VAX, and the IEEE floating point standard [144]. Most floating-point numbers fit in either a word (32 bits, or short floating representation), or a 64-bit double word operand. Floating-point numbers contain a sign specification, a representation of the fraction (mantissa or significand), and the exponent representationeither exponent plus sign or a characteristic in an excess code representation. A number of other aspects of a floating-point number are implied, i.e., understood |
|
|
|
|
|